Comprehensive study material for CBSE Class 11 Physics prepared by www.growupnect.com
Introduction to Units and Measurements
Physics is fundamentally about understanding and describing the natural world through measurement. Every physical quantity we encounter requires proper measurement, and for meaningful communication of these measurements, we need standardized units and measurements. This chapter forms the foundation of physics by establishing the framework for all quantitative analysis.
What are Physical Quantities?
Physical quantities are properties of matter and phenomena that can be measured and expressed numerically. Understanding units and measurements begins with categorizing these quantities:
Fundamental (Base) Quantities
These are independent quantities that cannot be expressed in terms of other quantities:
- Length – measures distance or size
- Mass – measures amount of matter
- Time – measures duration
- Electric Current – measures flow of charge
- Temperature – measures thermal state
- Amount of Substance – measures quantity of matter
- Luminous Intensity – measures brightness
Derived Quantities
These quantities are expressed in terms of fundamental quantities:
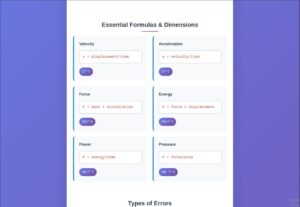
- Area = Length × Length
- Volume = Length³
- Velocity = Length ÷ Time
- Acceleration = Length ÷ Time²
- Force = Mass × Acceleration
- Pressure = Force ÷ Area
The International System of Units (SI)
The SI system is the modern metric system used globally for scientific measurements. Understanding units and measurements requires mastery of this system.
SI Base Units
| Physical Quantity | SI Unit | Symbol |
| Length | metre | m |
| Mass | kilogram | kg |
| Time | second | s |
| Electric Current | ampere | A |
| Temperature | kelvin | K |
| Amount of Substance | mole | mol |
| Luminous Intensity | candela | cd |
Important Derived Units
| Physical Quantity | Derived Unit | Symbol | Expression |
| Force | newton | N | kg⋅m⋅s⁻² |
| Energy | joule | J | kg⋅m²⋅s⁻² |
| Power | watt | W | kg⋅m²⋅s⁻³ |
| Pressure | pascal | Pa | kg⋅m⁻¹⋅s⁻² |
| Frequency | hertz | Hz | s⁻¹ |
Unit Prefixes and Scientific Notation
Units and measurements often involve very large or very small quantities. SI prefixes help express these efficiently:
Common SI Prefixes
| Prefix | Symbol | Factor | Example |
| tera | T | 10¹² | 1 THz = 10¹² Hz |
| giga | G | 10⁹ | 1 GB = 10⁹ bytes |
| mega | M | 10⁶ | 1 MHz = 10⁶ Hz |
| kilo | k | 10³ | 1 km = 10³ m |
| centi | c | 10⁻² | 1 cm = 10⁻² m |
| milli | m | 10⁻³ | 1 ms = 10⁻³ s |
| micro | μ | 10⁻⁶ | 1 μm = 10⁻⁶ m |
| nano | n | 10⁻⁹ | 1 nm = 10⁻⁹ m |
| pico | p | 10⁻¹² | 1 ps = 10⁻¹² s |
Measurement of Length
Standard Metre
The metre is defined as the distance light travels in vacuum in 1/299,792,458 seconds. This definition makes units and measurements extremely precise.
Measurement Techniques
- Direct Method: Using rulers, measuring tapes
- Parallax Method: For astronomical distances
- Triangulation: For large terrestrial distances
- Echolocation: Using sound waves
Length Scales in Universe
- Atomic scale: 10⁻¹⁰ m
- Human scale: 10⁰ m
- Terrestrial scale: 10⁶ m
- Astronomical scale: 10¹⁶ m
Measurement of Mass
Standard Kilogram
Originally defined by a platinum-iridium cylinder, now redefined using Planck’s constant for ultimate precision in units and measurements.
Mass Measurement Methods
- Beam Balance: Compares unknown mass with standard
- Spring Balance: Uses Hooke’s law
- Electronic Balance: Uses electromagnetic force
Mass Ranges
- Electron mass: 9.1 × 10⁻³¹ kg
- Proton mass: 1.67 × 10⁻²⁷ kg
- Human mass: ~70 kg
- Earth mass: 6.0 × 10²⁴ kg
Measurement of Time
Standard Second
Defined as 9,192,631,770 periods of radiation from cesium-133 atom transition, ensuring exceptional accuracy in units and measurements.
Time Measurement Devices
- Atomic Clocks: Most precise (accuracy: 1 part in 10¹³)
- Quartz Clocks: High precision for everyday use
- Pendulum Clocks: Historical importance
- Digital Watches: Common modern usage
Time Scales
- Atomic processes: 10⁻²² s
- Human lifetime: ~2 × 10⁹ s
- Age of universe: ~4 × 10¹⁷ s
Accuracy and Precision in Units and Measurements
Accuracy
Closeness of measured value to the true value. High accuracy means systematic errors are minimized.
Precision
Reproducibility of measurements. High precision means random errors are small.
Key Differences
- Measurements can be precise but not accurate
- Measurements can be accurate but not precise
- Ideal measurements are both accurate and precise
Errors in Measurement
Understanding errors is crucial for reliable units and measurements:
Types of Errors
1. Systematic Errors
- Instrumental Error: Due to faulty instruments
- Environmental Error: Due to external conditions
- Personal Error: Due to observer limitations
- Procedural Error: Due to incorrect methodology
2. Random Errors
- Unpredictable fluctuations
- Can be minimized by multiple measurements
- Follow statistical laws
3. Gross Errors
- Human mistakes
- Reading errors
- Calculation errors
Error Analysis Techniques
- Mean Value: x̄ = (x₁ + x₂ + … + xₙ)/n
- Absolute Error: Δx = |x – x̄|
- Relative Error: Δx/x̄
- Percentage Error: (Δx/x̄) × 100%
Significant Figures
Significant figures represent the precision of units and measurements:
Rules for Significant Figures
- All non-zero digits are significant
- Zeros between non-zero digits are significant
- Leading zeros are not significant
- Trailing zeros in decimal numbers are significant
- Trailing zeros in whole numbers may or may not be significant
Examples
- 45 → 5 significant figures
- 00456 → 3 significant figures
- 1200 → 2 or 4 significant figures (ambiguous)
- 200 × 10³ → 4 significant figures
Operations with Significant Figures
- Addition/Subtraction: Result has decimal places of least precise number
- Multiplication/Division: Result has significant figures of least precise number
Dimensional Analysis
Dimensions represent the physical nature of quantities in units and measurements:
Fundamental Dimensions
- Length: [L]
- Mass: [M]
- Time: [T]
- Current: [A]
- Temperature: [K]
- Amount: [mol]
- Luminous Intensity: [cd]
Dimensional Formulas
- Velocity: [LT⁻¹]
- Acceleration: [LT⁻²]
- Force: [MLT⁻²]
- Energy: [ML²T⁻²]
- Pressure: [ML⁻¹T⁻²]
Applications of Dimensional Analysis
- Checking equation validity
- Deriving relationships
- Converting units
- Estimating physical quantities
Limitations
- Cannot determine dimensionless constants
- Cannot handle exponential, logarithmic functions
- Cannot determine equation’s exact form
Practical Applications
Laboratory Measurements
- Use appropriate instruments for required precision
- Account for instrumental limitations
- Perform multiple readings
- Calculate and report uncertainties
Real-world Examples
- GPS: Requires precise time measurements
- Engineering: Dimensional analysis for design
- Medicine: Accurate dosage measurements
- Space missions: Extremely precise calculations
Problem-Solving Strategies
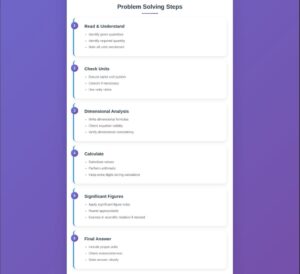
Step-by-Step Approach
- Identify given quantities and units
- Determine required quantity
- Apply dimensional analysis if needed
- Use appropriate conversion factors
- Check dimensional consistency
- Evaluate significant figures
- State final answer with proper units
Common Conversion Factors
- 1 km = 1000 m = 10³ m
- 1 cm = 0.01 m = 10⁻² m
- 1 g = 0.001 kg = 10⁻³ kg
- 1 hour = 3600 s
- 1 year ≈ 3.15 × 10⁷ s
Key Formulas and Relations
Error Calculations
- Mean: x̄ = Σxᵢ/n
- Standard deviation: σ = √[Σ(xᵢ – x̄)²/(n-1)]
- Percentage error: (Δx/x) × 100%
Unit Conversions
- Always multiply by unity ratios
- Cancel unwanted units systematically
- Check final dimensional consistency
Important Points to Remember
- Units and measurements form the foundation of all physics
- SI system provides international standardization
- Accuracy and precision are different concepts
- Errors are inevitable but can be minimized
- Significant figures indicate measurement precision
- Dimensional analysis is a powerful problem-solving tool
- Proper unit conversion is essential for correct results
Practice Questions Guide
Type 1: Unit Conversion
Convert between different unit systems maintaining significant figures
Type 2: Error Analysis
Calculate absolute, relative, and percentage errors from given data
Type 3: Dimensional Analysis
Derive relationships and check equation validity
Type 4: Significant Figures
Apply rules in calculations and express results correctly
Conclusion
Mastering units and measurements is essential for success in physics. This chapter provides the tools for accurate measurement, error analysis, and proper expression of physical quantities. These concepts will be applied throughout your physics studies and are fundamental to scientific thinking.
The precision and standardization of units and measurements enable global scientific collaboration and technological advancement. From the smallest atomic scales to vast cosmic distances, proper measurement techniques allow us to understand and describe our universe quantitatively.
Remember: Physics is ultimately about measurement, and measurement requires a thorough understanding of units and measurements.
Frequently Asked Questions (FAQs) – Units and Measurements
Q1. What is the difference between fundamental and derived units?
Answer: Fundamental units are independent basic units that cannot be expressed in terms of other units (like metre, kilogram, second). Derived units are formed by combining fundamental units (like m/s for velocity, kg⋅m/s² for force).
Q2. Why is the SI system important in units and measurements?
Answer: SI system provides global standardization, making scientific communication universal. It ensures consistency in measurements worldwide and eliminates confusion between different measurement systems.
Q3. How many significant figures should I use in my calculations?
Answer: The result should have the same number of significant figures as the measurement with the least significant figures. For addition/subtraction, consider decimal places; for multiplication/division, consider significant figures.
Q4. What is the most precise method for measuring time?
Answer: Atomic clocks are the most precise, with accuracy of 1 part in 10¹³. They use cesium-133 atomic transitions and are used for defining the standard second in units and measurements.
Q5. How do I convert units properly?
Answer: Use the unity ratio method: multiply by conversion factors equal to 1. For example, to convert km to m, multiply by (1000 m/1 km). Always cancel units algebraically.
Q6. What are the main sources of errors in measurement?
Answer: Three main types: Systematic errors (instrumental, environmental, personal), Random errors (unpredictable fluctuations), and Gross errors (human mistakes in reading or calculation).
Q7. How is the metre currently defined?
Answer: The metre is defined as the distance light travels in vacuum in 1/299,792,458 of a second. This definition makes units and measurements extremely precise and reproducible.
Q8. What is dimensional analysis and why is it useful?
Answer: Dimensional analysis uses the dimensions of physical quantities to check equations, derive relationships, and solve problems. It’s useful for checking formula validity and converting between unit systems.
Q9. Can measurements be precise but not accurate?
Answer: Yes! Precision refers to reproducibility (consistent results), while accuracy refers to closeness to true value. You can have consistent wrong measurements (precise but inaccurate).
Q10. What are the seven fundamental quantities in SI system?
Answer: Length (metre), Mass (kilogram), Time (second), Electric current (ampere), Temperature (kelvin), Amount of substance (mole), and Luminous intensity (candela).
Q11. How do I handle zeros in significant figures?
Answer: Leading zeros are never significant. Zeros between non-zero digits are always significant. Trailing zeros are significant only if there’s a decimal point shown.
Q12. What is the importance of units and measurements in daily life?
Answer: Units and measurements are essential for cooking recipes, medical dosages, construction, GPS navigation, fuel efficiency, and virtually every aspect of modern life requiring precision.
Q13. How can I minimize errors in laboratory measurements?
Answer: Take multiple readings, use appropriate instruments, calibrate equipment, control environmental conditions, and always calculate and report uncertainties properly.
Q14. What is the relationship between accuracy and precision?
Answer: Accuracy is how close you are to the true value, while precision is how close your repeated measurements are to each other. Ideal measurements are both accurate and precise.
Q15. Why can’t dimensional analysis determine numerical constants?
Answer: Dimensional analysis only checks the dimensional consistency of equations but cannot determine dimensionless numerical factors, which must be found through experiments or theoretical derivations.
These comprehensive notes on Units and Measurements for Class 11 Physics are prepared by www.growupnect.com to help students excel in their studies. Practice regularly and apply these concepts to build a strong foundation in physics.



