Ganita Prakash Class 6 maths chapter 1 solutions

Page 2: Figure it Out

1. Can you think of other examples where mathematics helps us in our everyday lives?

Mathematics is used everywhere! Here are some simple examples:

Shopping: You calculate the total cost of items or check if you have enough money.
Cooking: You measure ingredients (like 2 cups of flour) or set a timer for baking.
Time Management: You use clocks and calendars to plan your day, like knowing when to go to school.
Games: In sports, you count scores, or in board games, you use numbers to move pieces.

2. How has mathematics helped propel humanity forward?

Mathematics has helped in many big ways:

Scientific Experiments: Math helps measure things, like how fast a chemical reaction happens.
Economy and Democracy: Math is used to count votes in elections or manage money in banks.
Building Structures: Math helps design bridges, houses, and tall buildings to make them safe.
Technology: Math is used to make TVs, phones, computers, cars, planes, and even clocks.

Page 3: Figure it Out

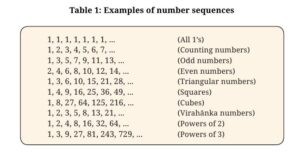
1. Can you recognize the pattern in each of the sequences in Table 1?

Let’s look at each sequence in Table 1 and find the pattern:

1, 1, 1, 1, 1, 1, … (All 1’s): Every number is 1. The pattern is that it stays 1 forever.
1, 2, 3, 4, 5, 6, 7, … (Counting numbers): Each number increases by 1. It’s just counting: 1, 2, 3, and so on.
1, 3, 5, 7, 9, 11, 13, … (Odd numbers): These are numbers that can’t be divided by 2 evenly. Each number increases by 2 (1 + 2 = 3, 3 + 2 = 5, etc.).
2, 4, 6, 8, 10, 12, 14, … (Even numbers): These are numbers divisible by 2. Each number increases by 2 (2 + 2 = 4, 4 + 2 = 6, etc.).
1, 3, 6, 10, 15, 21, 28, … (Triangular numbers): Each number is the sum of counting numbers: 1 = 1, 1+2 = 3, 1+2+3 = 6, 1+2+3+4 = 10, and so on.
1, 4, 9, 16, 25, 36, 49, … (Squares): These are numbers multiplied by themselves: 1×1 = 1, 2×2 = 4, 3×3 = 9, 4×4 = 16, etc.
1, 8, 27, 64, 125, 216, … (Cubes): These are numbers multiplied by themselves twice: 1×1×1 = 1, 2×2×2 = 8, 3×3×3 = 27, etc.
1, 2, 3, 5, 8, 13, 21, … (Virahānka numbers): Each number is the sum of the previous two numbers: 1+2 = 3, 2+3 = 5, 3+5 = 8, and so on.
1, 2, 4, 8, 16, 32, 64, … (Powers of 2): Each number is 2 multiplied by itself: 2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16, etc.
1, 3, 9, 27, 81, 243, 729, … (Powers of 3): Each number is 3 multiplied by itself: 3¹ = 3, 3² = 9, 3³ = 27, 3⁴ = 81, etc.

2. Rewrite each sequence of Table 1 in your notebook, along with the next three numbers in each sequence! After each sequence, write in your own words what is the rule for forming the numbers in the sequence.

Let’s write each sequence, find the next three numbers, and explain the rule:

All 1’s: 1, 1, 1, 1, 1, 1, …
- Next three numbers: 1, 1, 1 (it’s always 1).
- Rule: Every number in this sequence is just 1, and it never changes.
Counting numbers: 1, 2, 3, 4, 5, 6, 7, …
- Next three numbers: 8, 9, 10 (7+1 = 8, 8+1 = 9, 9+1 = 10).
- Rule: Start with 1 and add 1 each time to get the next number.
Odd numbers: 1, 3, 5, 7, 9, 11, 13, …
- Next three numbers: 15, 17, 19 (13+2 = 15, 15+2 = 17, 17+2 = 19).
- Rule: Start with 1 and add 2 each time to get the next odd number.
Even numbers: 2, 4, 6, 8, 10, 12, 14, …
- Next three numbers: 16, 18, 20 (14+2 = 16, 16+2 = 18, 18+2 = 20).
- Rule: Start with 2 and add 2 each time to get the next even number.
Triangular numbers: 1, 3, 6, 10, 15, 21, 28, …
- Next three numbers: 36, 45, 55 (28+8 = 36, 36+9 = 45, 45+10 = 55).
- Rule: Add the next counting number each time (1+2 = 3, 3+3 = 6, 6+4 = 10, etc.).
Squares: 1, 4, 9, 16, 25, 36, 49, …
- Next three numbers: 64, 81, 100 (8×8 = 64, 9×9 = 81, 10×10 = 100).
- Rule: Multiply a number by itself (1×1, 2×2, 3×3, etc.).
Cubes: 1, 8, 27, 64, 125, 216, …
- Next three numbers: 343, 512, 729 (7×7×7 = 343, 8×8×8 = 512, 9×9×9 = 729).
- Rule: Multiply a number by itself twice (1×1×1, 2×2×2, 3×3×3, etc.).
Virahānka numbers: 1, 2, 3, 5, 8, 13, 21, …
- Next three numbers: 34, 55, 89 (21+13 = 34, 34+21 = 55, 55+34 = 89).
- Rule: Add the last two numbers to get the next one (1+2 = 3, 2+3 = 5, etc.).
Powers of 2: 1, 2, 4, 8, 16, 32, 64, …
- Next three numbers: 128, 256, 512 (64×2 = 128, 128×2 = 256, 256×2 = 512).
- Rule: Start with 1 and multiply by 2 each time.
Powers of 3: 1, 3, 9, 27, 81, 243, 729, …
- Next three numbers: 2187, 6561, 19683 (729×3 = 2187, 2187×3 = 6561, 6561×3 = 19683).
- Rule: Start with 1 and multiply by 3 each time.

Page 5: Figure it Out

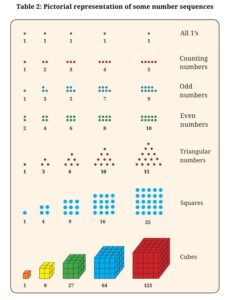
1. Copy the pictorial representations of the number sequences in Table 2 in your notebook, and draw the next picture for each sequence!

Since Table 2 (pictorial representations) isn’t shown in the document, we can’t draw the pictures. However, the document mentions that the first seven sequences from Table 1 are represented pictorially. These are: All 1’s, Counting numbers, Odd numbers, Even numbers, Triangular numbers, Squares, and Cubes. You would need to:

Imagine dots or shapes representing each sequence (e.g., triangular numbers as triangles, squares as square grids).
Draw the next picture by adding the next number in the sequence (like we calculated above).

2. Why are 1, 3, 6, 10, 15, … called triangular numbers? Why are 1, 4, 9, 16, 25, … called square numbers or squares? Why are 1, 8, 27, 64, 125, … called cubes?

Triangular numbers (1, 3, 6, 10, 15, …): They are called triangular because you can arrange their dots in the shape of a triangle. For example, 3 dots can be arranged as:
```
*
**
```
And 6 dots as:
```
*
**
***
```
Square numbers (1, 4, 9, 16, 25, …): They are called squares because you can arrange their dots in a square shape. For example, 4 dots can be arranged as:
```
**
**
```
And 9 dots as:
```
***
***
***
```
Cubes (1, 8, 27, 64, 125, …): They are called cubes because they represent the number of small cubes in a larger cube. For example, 8 small cubes (2×2×2) make a larger cube of side 2, and 27 small cubes (3×3×3) make a larger cube of side 3.

3. 36 is both a triangular number and a square number! That is, 36 dots can be arranged perfectly both in a triangle and in a square. Make pictures in your notebook illustrating this!

As a triangular number: 36 is the 8th triangular number (1+2+3+…+8 = 36). Arrange 36 dots in a triangle:
```
*
**
***
****
*****
******
*******
********
```
As a square number: 36 is 6×6. Arrange 36 dots in a square:
```
******
******
******
******
******
******
```

4. What would you call the following sequence of numbers: 1, 19, 37?

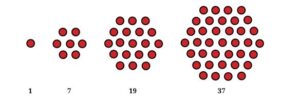
That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?

Hexagonal numbers: These numbers can be arranged in a hexagon shape. The sequence is 1, 19, 37.
Pattern: Let’s find the difference:
- 19 – 1 = 18
- 37 – 19 = 18 The difference is 18 each time. So, the next number is 37 + 18 = 55.
Draw: You can draw hexagons with 1 dot, 19 dots, and 37 dots (as layers of a hexagon), but since we can’t draw here, imagine a hexagon shape growing with more dots.

5. Can you think of pictorial ways to visualize the sequence of Powers of 2? Powers of 3?

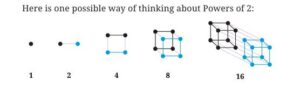
Powers of 2 (1, 2, 4, 8, 16, …): Imagine a tree that doubles its branches each time. Start with 1 dot, then 2 dots (split into two), then 4 dots (each splits into two), and so on.
Powers of 3 (1, 3, 9, 27, …): Imagine a triangle that triples its size. Start with 1 dot, then 3 dots in a triangle, then 9 dots in a larger triangle, and so on.

Page 7: Figure it Out

1. By drawing a similar picture, can you say what is the sum of the first 10 odd numbers?

The document shows that adding odd numbers gives square numbers:

1 = 1 (1²)
1+3 = 4 (2²)
1+3+5 = 9 (3²)
And so on, up to 1+3+5+7+9+11 = 36 (6²). The pattern is: the sum of the first $n$

odd numbers is

$n²$

.
First 10 odd numbers: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19.
Sum = $10² = 100$

.

2. Now by imagining a similar picture, or by drawing it partially, as needed, can you say what is the sum of the first 100 odd numbers?

Using the same pattern:

Sum of the first 100 odd numbers = $100² = 10000$

.

Page 8: Figure it Out

1. Can you find a similar pictorial explanation for why adding counting numbers up and down, i.e., 1, 1+2+1, 1+2+3+2+1, …, gives square numbers?

The sequence is:

1 = 1 (1²)
1+2+1 = 4 (2²)
1+2+3+2+1 = 9 (3²)
1+2+3+4+3+2+1 = 16 (4²) Pictorial explanation: Imagine a square grid of dots:
For $n=2$

, the sum is 1+2+1 = 4. Draw a 2×2 square (4 dots). The “1” is the top-left dot, “2” is the top-right and bottom-left dots, and the last “1” is the bottom-right dot.
For $n=3$

, the sum is 1+2+3+2+1 = 9. Draw a 3×3 square (9 dots). The “1” is the top-left corner, “2” is the next two dots, “3” is the middle row, and so on.

2. By imagining a large version of your picture, or drawing it partially, as needed, can you see what will be the value of 1+2+3+…+99+100+99+…+3+2+1?

This is the sum for

$n=100$

Sum = $1 + 2 + 3 + \ldots + 99 + 100 + 99 + \ldots + 3 + 2 + 1$

. From the pattern, the sum is

$n²$

, so for

$n=100$

:
Sum = $100² = 10000$

.

3. Which sequence do you get when you start to add the All 1’s sequence up? What sequence do you get when you add the All 1’s sequence up and down?

Adding All 1’s up:
- 1 = 1
- 1+1 = 2
- 1+1+1 = 3
- This gives the counting numbers: 1, 2, 3, 4, ….
Adding All 1’s up and down:
- 1 = 1
- 1+1 = 2
- 1+1+1 = 3
- This is the same as adding up, because there’s no “down” part (since it’s all 1’s). So, it’s still the counting numbers: 1, 2, 3, 4, ….

4. Which sequence do you get when you start to add the counting numbers up? Can you give a smaller pictorial explanation?

Adding counting numbers up:
- 1 = 1
- 1+2 = 3
- 1+2+3 = 6
- 1+2+3+4 = 10
- This gives the triangular numbers: 1, 3, 6, 10, ….
Pictorial explanation: Draw dots in a triangle:
- 1 dot: *
- 1+2 = 3 dots: * **
- 1+2+3 = 6 dots: * ** ***

5. What happens when you add up pairs of consecutive triangular numbers? That is, take 1+3, 3+6, 6+10, 10+15, … Which sequence do you get? Why? Can you explain it with a picture?

Pairs of triangular numbers:
- 1+3 = 4
- 3+6 = 9
- 6+10 = 16
- 10+15 = 25
This gives the square numbers: 4, 9, 16, 25, ….
Why?: Each pair adds up to $n²$

. For example, the

$n$

-th triangular number is

$\frac{n(n+1)}{2}$

, and the

$(n+1)$

-th is

$\frac{(n+1)(n+2)}{2}$

. Adding them often results in a square.
Picture: Draw two triangles and put them together to form a square. For example, 6 and 10 dots can be arranged to form a 4×4 square (16 dots).

6. What happens when you start to add up powers of 2 starting with 1, i.e., take 1, 1+2, 1+2+4, 1+2+4+8, …? Now add 1 to each of these numbers—what numbers do you get? Why does this happen?

Adding powers of 2:
- 1 = 1
- 1+2 = 3
- 1+2+4 = 7
- 1+2+4+8 = 15
- Pattern: $1 + 2 + 4 + \ldots + 2^n = 2^{n+1} – 1$
  
  . So, 1, 3, 7, 15, ….
Add 1 to each:
- 1+1 = 2
- 3+1 = 4
- 7+1 = 8
- 15+1 = 16
- This gives the powers of 2: 2, 4, 8, 16, ….
Why?: Adding powers of 2 gives $2^{n+1} – 1$

, and adding 1 makes it

$2^{n+1}$

, which is the next power of 2.

7. What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Can you explain it with a picture?

Triangular numbers × 6 + 1:
- 1 × 6 + 1 = 7
- 3 × 6 + 1 = 19
- 6 × 6 + 1 = 37
- 10 × 6 + 1 = 61
This gives the hexagonal numbers: 7, 19, 37, 61, … (note: the document says 1, 19, 37, but this might be a typo in the sequence starting point).
Picture: Hexagonal numbers can be arranged in a hexagon. Multiplying by 6 and adding 1 relates to the structure of hexagons.

8. What happens when you start to add up hexagonal numbers, i.e., take 1, 1+7, 1+7+19, 1+7+19+37, …? Which sequence do you get? Can you explain it using a picture of a cube?

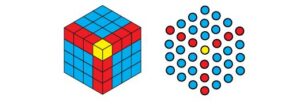
Adding hexagonal numbers (assuming the sequence 1, 7, 19, 37, …):
- 1 = 1
- 1+7 = 8
- 1+7+19 = 27
- 1+7+19+37 = 64
This gives the cubes: 1, 8, 27, 64, ….
Picture: Hexagonal numbers can be stacked to form a cube. For example, 1+7+19 = 27 (3×3×3), which is a cube of side 3.

9. Find your own patterns or relations in and among the sequences in Table 1. Can you explain why they happen with a picture or otherwise?

Pattern: Add pairs of Virahānka numbers:
- 1+2 = 3
- 2+3 = 5
- 3+5 = 8
- This gives the Virahānka numbers again (shifted): 3, 5, 8, ….
Why?: The Virahānka sequence (Fibonacci) has the property that each number is the sum of the two before it, so adding consecutive pairs just shifts the sequence.

Page 11: Figure it Out

1. Can you recognize the pattern in each of the sequences in Table 3?

Table 3 isn’t shown, but the document mentions:

Regular Polygons: Triangle (3 sides), Square (4 sides), Pentagon (5 sides), ….
Complete Graphs: Graphs with increasing lines.
Stacked Squares/Triangles: Squares or triangles stacked to form larger shapes.
Koch Snowflake: A fractal shape. The pattern is the growth in the number of sides, lines, or smaller shapes.

2. Try and redraw each sequence in Table 3 in your notebook. Can you draw the next shape in each sequence? Why or why not? After each sequence, describe in your own words what is the rule or pattern for forming the shapes in the sequence.

Regular Polygons: Start with a triangle (3 sides), then a square (4 sides), then a pentagon (5 sides). Next shape: Hexagon (6 sides). Rule: Add 1 side each time.
Complete Graphs: Each vertex connects to all others. Rule: Add a vertex and connect it to all previous ones.
Stacked Squares/Triangles: Add more squares/triangles in a pattern (e.g., rows). Rule: Add a row with more shapes.
Koch Snowflake: Replace each line with a “speed bump” shape. Rule: Repeat the replacement process.

Page 11-12: Figure it Out

1. Count the number of sides in each shape in the sequence of Regular Polygons. Which number sequence do you get? What about the number of corners in each shape in the sequence of Regular Polygons? Do you get the same number sequence? Can you explain why this happens?

Number of sides: Triangle (3), Square (4), Pentagon (5), … → 3, 4, 5, 6, … (Counting numbers starting from 3).
Number of corners: Same as sides: 3, 4, 5, 6, ….
Why?: In a polygon, the number of sides equals the number of corners (vertices). For example, a triangle has 3 sides and 3 corners.

2. Count the number of lines in each shape in the sequence of Complete Graphs. Which number sequence do you get? Can you explain why?

In a complete graph with $n$

vertices, every vertex connects to every other vertex.
Number of lines = $\frac{n(n-1)}{2}$

:
- $n=2$
  
  : 1 line
- $n=3$
  
  : 3 lines
- $n=4$
  
  : 6 lines
- $n=5$
  
  : 10 lines
Sequence: 1, 3, 6, 10, … (Triangular numbers).
Why?: The number of lines is the number of ways to choose 2 vertices out of $n$

, which is the formula for triangular numbers.

3. How many little squares are there in each shape of the sequence of Stacked Squares? Which number sequence does this give? Can you explain why?

Stacked Squares: Imagine a grid growing by adding rows and columns.
If it’s an $n \times n$

grid:
- $n=1$
  
  : 1 square
- $n=2$
  
  : 4 little squares
- $n=3$
  
  : 9 little squares
Sequence: 1, 4, 9, … (Square numbers).
Why?: An $n \times n$

grid has

$n²$

little 1×1 squares.

4. How many little triangles are there in each shape of the sequence of Stacked Triangles? Which number sequence does this give? Can you explain why? (Hint: In each shape in the sequence, how many triangles are there in each row?)

Stacked Triangles: Imagine a big triangle made of smaller triangles.
If there are $n$

rows:
- Row 1: 1 triangle
- Row 2: 2 triangles
- Row 3: 3 triangles
- Total = 1 + 2 + 3 + … + $n$
  
  .
For $n=1, 2, 3, …$

:
- $n=1$
  
  : 1 triangle
- $n=2$
  
  : 1+2 = 3 triangles
- $n=3$
  
  : 1+2+3 = 6 triangles
Sequence: 1, 3, 6, … (Triangular numbers).
Why?: The number of small triangles in $n$

rows is the sum of the first

$n$

counting numbers, which is a triangular number.

5. To get from one shape to the next shape in the Koch Snowflake sequence, one replaces each line segment ‘~’ by a ‘speed bump’ ~. As one does this more and more times, the changes become tinier and tinier with very very small line segments. How many total line segments are there in each shape of the Koch Snowflake? What is the corresponding number sequence?

Koch Snowflake:
- Start with a triangle (3 sides): 3 segments.
- Step 1: Each segment becomes 4 segments (replace ~ with ~). Total = $3 \times 4 = 12$
  
  .
- Step 2: Each of the 12 segments becomes 4 segments. Total = $12 \times 4 = 48$
  
  .
Sequence: 3, 12, 48, ….
Pattern: Each step multiplies the previous number by 4. So, it’s $3 \times 4^n$

, which is 3 times the powers of 4.

That’s the solution to all the questions in simple language! If you need more help with any part, let me know.

Article: Unlock Ganita Prakash Class 6 Solutions for Chapter 1 – Patterns in Mathematics

Are you a Class 6 student struggling with Chapter 1 of your Maths textbook, Ganita Prakash? Or perhaps a parent looking to help your child understand number patterns and shapes? Look no further! In this guide, we’ll dive into Ganita Prakash Class 6 solutions for Chapter 1, “Patterns in Mathematics,” and break down the concepts in a simple, easy-to-understand way. Let’s explore number sequences, shape patterns, and more, with step-by-step explanations.

What’s in Chapter 1 of Ganita Prakash Class 6?

Chapter 1 of Ganita Prakash Grade 6 introduces students to the fascinating world of patterns in mathematics. It explains how mathematics is all about finding patterns and understanding why they exist. Here’s what you’ll learn:

Number Sequences: Discover sequences like counting numbers (1, 2, 3, …), odd numbers (1, 3, 5, …), triangular numbers (1, 3, 6, …), square numbers (1, 4, 9, …), and even Virahānka numbers (1, 2, 3, 5, …).
Visualizing Patterns: Learn how to draw pictures to understand sequences, like arranging dots into triangles or squares.
Shape Patterns: Explore shape sequences like regular polygons (triangle, square, pentagon, …) and Koch snowflakes.
Real-Life Applications: See how mathematics helps in everyday life, from building bridges to launching rockets to the Moon!

Why Choose Ganita Prakash Class 6 Solutions?

The Ganita Prakash textbook is designed to make math fun and creative for Class 6 students. But sometimes, the “Figure it Out” questions can be tricky. That’s where our Ganita Prakash Class 6 solutions come in! We provide clear answers to all the questions in Chapter 1, helping you understand the patterns and their explanations.

Key Concepts and Solutions from Chapter 1

Let’s look at some important concepts and their solutions:

Number Sequences and Patterns
- The chapter lists sequences like triangular numbers (1, 3, 6, 10, …) and square numbers (1, 4, 9, 16, …).
- Solution Example: To find the next three triangular numbers after 1, 3, 6, 10, 15, 21, 28, you add the next counting numbers: 28 + 8 = 36, 36 + 9 = 45, 45 + 10 = 55. So, the next three numbers are 36, 45, 55.
- Why It’s Called Triangular: You can arrange the dots in a triangle shape, like 6 dots as:
```
*
**
***
```
Adding Odd Numbers to Get Squares
- The chapter shows that adding odd numbers gives square numbers: 1 + 3 = 4, 1 + 3 + 5 = 9, 1 + 3 + 5 + 7 = 16, and so on.
- Solution Example: What’s the sum of the first 10 odd numbers? It’s 10² = 100. So, 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100.
Hexagonal Numbers and More
- Hexagonal numbers like 1, 19, 37, … are introduced.
- Solution Example: The next hexagonal number after 1, 19, 37 is 37 + 18 = 55. These numbers can be drawn as hexagons, growing layer by layer.
Shape Patterns
- Regular polygons start with a triangle (3 sides), then a square (4 sides), and so on.
- Solution Example: The number of sides in regular polygons follows the sequence 3, 4, 5, 6, …, which is the counting numbers starting from 3.

How to Use These Solutions for Better Learning

Understand the Concept First: Read the chapter in Ganita Prakash Grade 6 to learn about patterns and why they matter.
Practice with Pictures: Draw the sequences (like triangular or square numbers) to see the patterns visually.
Solve Questions: Use our solutions to check your answers to the “Figure it Out” questions.
Apply in Real Life: Think about how math patterns help in daily life, like designing a calendar or building a bridge.

Download Ganita Prakash Class 6 Chapter 1 PDF with Solutions

Looking for a Class 6 Maths Chapter 1 PDF with answers? While we can’t provide the PDF directly, you can find the official Ganita Prakash Grade 6 textbook from your school or online portals like NCERT’s website. Use our solutions to understand the chapter better and ace your exams!

Why Patterns Matter in Mathematics

Patterns are the heart of mathematics. As Ganita Prakash explains, understanding patterns helps us solve problems in science, technology, and even art. For example, the patterns in the motion of planets helped humans develop rockets, while patterns in numbers help us design computers and clocks.

Conclusion

With our Ganita Prakash Class 6 solutions for Chapter 1, you’ll master patterns in mathematics in no time! Whether it’s number sequences like triangular numbers or shape patterns like regular polygons, we’ve got you covered. Start exploring the creativity of math today, and watch your skills grow.

Meta Description

“Discover Ganita Prakash Class 6 solutions for Chapter 1 – Patterns in Mathematics. Get step-by-step answers to number sequences, shape patterns, and more. Perfect for students and parents!”

Searchable Keywords

Ganita Prakash Class 6 solutions
Class 6 Maths Chapter 1 solutions
Ganita Prakash Grade 6 Chapter 1
NCERT Class 6 Maths Chapter 1 PDF
Class 6 Maths Chapter 1 PDF with answers
Class 6 Maths Chapter 1 worksheet
Triangular numbers Class 6
Square numbers Class 6
Virahānka numbers explained
Regular polygons Class 6

Image Keywords (for SEO)

Ganita Prakash Class 6 solutions PDF
Triangular numbers diagram Class 6
Square numbers visual representation
Class 6 Maths Chapter 1 patterns
Hexagonal numbers drawing
Regular polygons illustration
Koch snowflake sequence Class 6
Number sequences visual Class 6
Ganita Prakash Grade 6 textbook image
Class 6 Maths Chapter 1 worksheet PDF